In order to obtain honest performance estimates for a learner all parts of the model building like preprocessing and model selection steps should be included in the resampling, i.e., repeated for every pair of training/test data. For steps that themselves require resampling like parameter tuning or feature selection (via the wrapper approach) this results in two nested resampling loops.
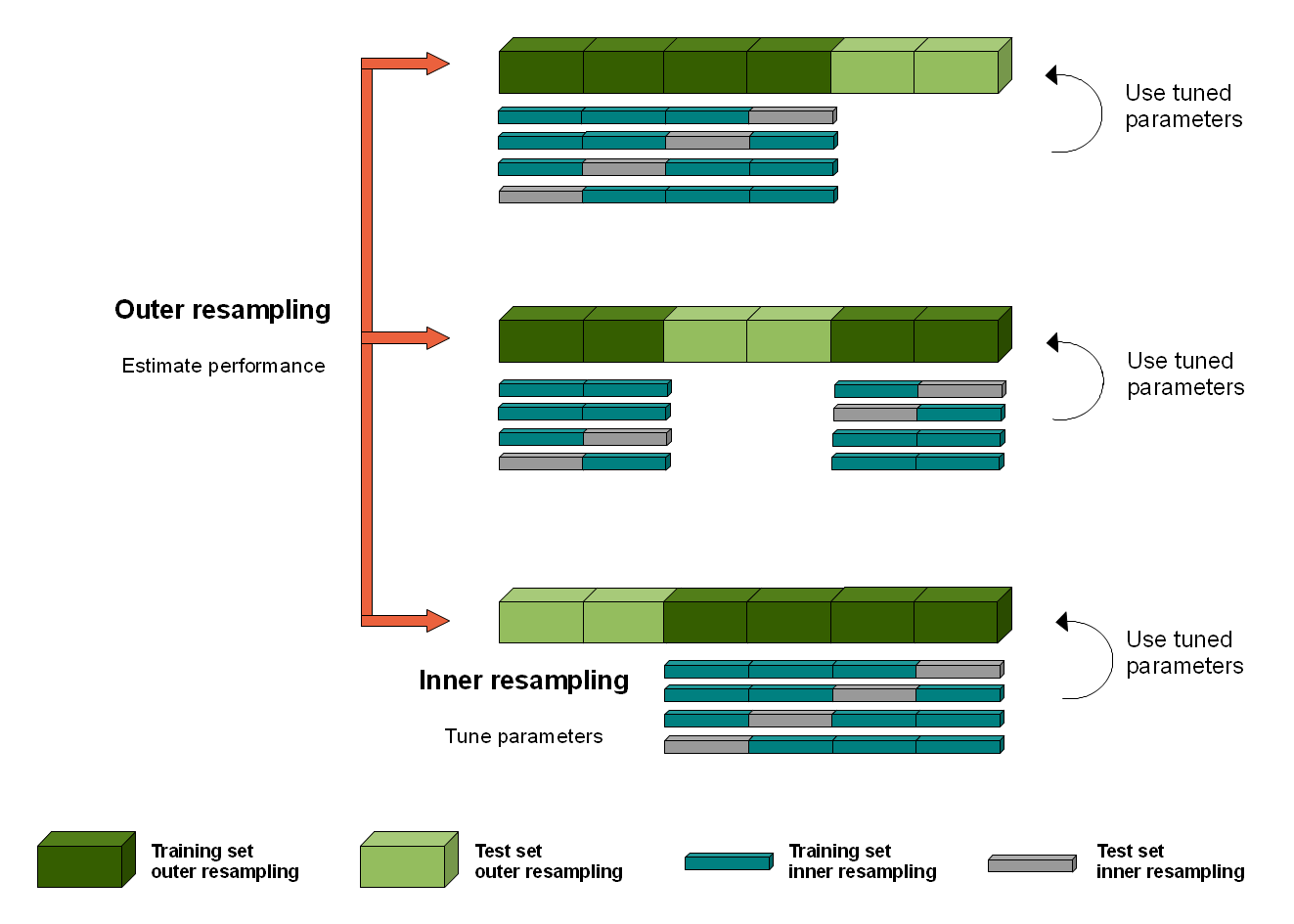
Nested Resampling Figure
The graphic above illustrates nested resampling for parameter tuning with 3-fold cross-validation in the outer and 4-fold cross-validation in the inner loop.
In the outer resampling loop, we have three pairs of training/test sets. On each of these outer training sets parameter tuning is done, thereby executing the inner resampling loop. This way, we get one set of selected hyperparameters for each outer training set. Then the learner is fitted on each outer training set using the corresponding selected hyperparameters and its performance is evaluated on the outer test sets.
In mlr, you can get nested resampling for free without programming any looping by using the wrapper functionality. This works as follows:
- Generate a wrapped Learner (
makeLearner()) via functionmakeTuneWrapper()ormakeFeatSelWrapper(). Specify the inner resampling strategy using theirresamplingargument. - Call function
resample()(see also the section about resampling and pass the outer resampling strategy to itsresamplingargument.
You can freely combine different inner and outer resampling strategies.
The outer strategy can be a resample description ResampleDesc (makeResampleDesc())) or a resample instance (makeResampleInstance())). A common setup is prediction and performance evaluation on a fixed outer test set. This can be achieved by using function makeFixedHoldoutInstance() to generate the outer resample instance(makeResampleInstance()`).
The inner resampling strategy should preferably be a ResampleDesc (makeResampleDesc()), as the sizes of the outer training sets might differ. Per default, the inner resample description is instantiated once for every outer training set. This way during tuning/feature selection all parameter or feature sets are compared on the same inner training/test sets to reduce variance. You can also turn this off using the same.resampling.instance argument of makeTuneControl* (TuneControl()) or makeFeatSelControl* (FeatSelControl()).
Nested resampling is computationally expensive. For this reason in the examples shown below we use relatively small search spaces and a low number of resampling iterations. In practice, you normally have to increase both. As this is computationally intensive you might want to have a look at section parallelization.
Tuning
As you might recall from the tutorial page about tuning, you need to define a search space by function ParamHelpers::makeParamSet(), a search strategy by makeTuneControl*(TuneControl()), and a method to evaluate hyperparameter settings (i.e., the inner resampling strategy and a performance measure).
Below is a classification example. We evaluate the performance of a support vector machine (kernlab::ksvm()) with tuned cost parameter C and RBF kernel parameter sigma. We use 3-fold cross-validation in the outer and subsampling with 2 iterations in the inner loop. For tuing a grid search is used to find the hyperparameters with lowest error rate (mmce is the default measure for classification). The wrapped Learner (makeLearner()) is generated by calling makeTuneWrapper().
Note that in practice the parameter set should be larger. A common recommendation is 2^(-12:12) for both C and sigma.
# Tuning in inner resampling loop
ps = makeParamSet(
makeDiscreteParam("C", values = 2^(-2:2)),
makeDiscreteParam("sigma", values = 2^(-2:2))
)
ctrl = makeTuneControlGrid()
inner = makeResampleDesc("Subsample", iters = 2)
lrn = makeTuneWrapper("classif.ksvm", resampling = inner, par.set = ps, control = ctrl, show.info = FALSE)
# Outer resampling loop
outer = makeResampleDesc("CV", iters = 3)
r = resample(lrn, iris.task, resampling = outer, extract = getTuneResult, show.info = FALSE)
r
## Resample Result
## Task: iris-example
## Learner: classif.ksvm.tuned
## Aggr perf: mmce.test.mean=0.0400000
## Runtime: 5.50584You can obtain the error rates on the 3 outer test sets by:
r$measures.test
## iter mmce
## 1 1 0.06
## 2 2 0.04
## 3 3 0.02Accessing the tuning result
We have kept the results of the tuning for further evaluations. For example one might want to find out, if the best obtained configurations vary for the different outer splits. As storing entire models may be expensive (but possible by setting models = TRUE) we used the extract option of resample(). Function getTuneResult() returns, among other things, the optimal hyperparameter values and the optimization path (ParamHelpers::OptPath()) for each iteration of the outer resampling loop. Note that the performance values shown when printing r$extract are the aggregated performances resulting from inner resampling on the outer training set for the best hyperparameter configurations (not to be confused with r$measures.test shown above).
r$extract
## [[1]]
## Tune result:
## Op. pars: C=1; sigma=0.5
## mmce.test.mean=0.0294118
##
## [[2]]
## Tune result:
## Op. pars: C=2; sigma=0.25
## mmce.test.mean=0.0294118
##
## [[3]]
## Tune result:
## Op. pars: C=2; sigma=0.25
## mmce.test.mean=0.0147059
names(r$extract[[1]])
## [1] "learner" "control" "x" "y" "resampling"
## [6] "threshold" "opt.path"We can compare the optimal parameter settings obtained in the 3 resampling iterations. As you can see, the optimal configuration usually depends on the data. You may be able to identify a range of parameter settings that achieve good performance though, e.g., the values for C should be at least 1 and the values for sigma should be between 0 and 1.
With function getNestedTuneResultsOptPathDf() you can extract the optimization paths for the 3 outer cross-validation iterations for further inspection and analysis. These are stacked in one data.frame with column iter indicating the resampling iteration.
opt.paths = getNestedTuneResultsOptPathDf(r)
head(opt.paths, 10)
## C sigma mmce.test.mean dob eol error.message exec.time iter
## 1 0.25 0.25 0.10294118 1 NA <NA> 1.463 1
## 2 0.5 0.25 0.11764706 2 NA <NA> 0.036 1
## 3 1 0.25 0.07352941 3 NA <NA> 0.043 1
## 4 2 0.25 0.07352941 4 NA <NA> 0.040 1
## 5 4 0.25 0.08823529 5 NA <NA> 0.042 1
## 6 0.25 0.5 0.13235294 6 NA <NA> 0.041 1
## 7 0.5 0.5 0.07352941 7 NA <NA> 0.043 1
## 8 1 0.5 0.07352941 8 NA <NA> 0.042 1
## 9 2 0.5 0.07352941 9 NA <NA> 0.037 1
## 10 4 0.5 0.10294118 10 NA <NA> 0.042 1Below we visualize the opt.paths for the 3 outer resampling iterations.
g = ggplot(opt.paths, aes(x = C, y = sigma, fill = mmce.test.mean))
g + geom_tile() + facet_wrap(~iter)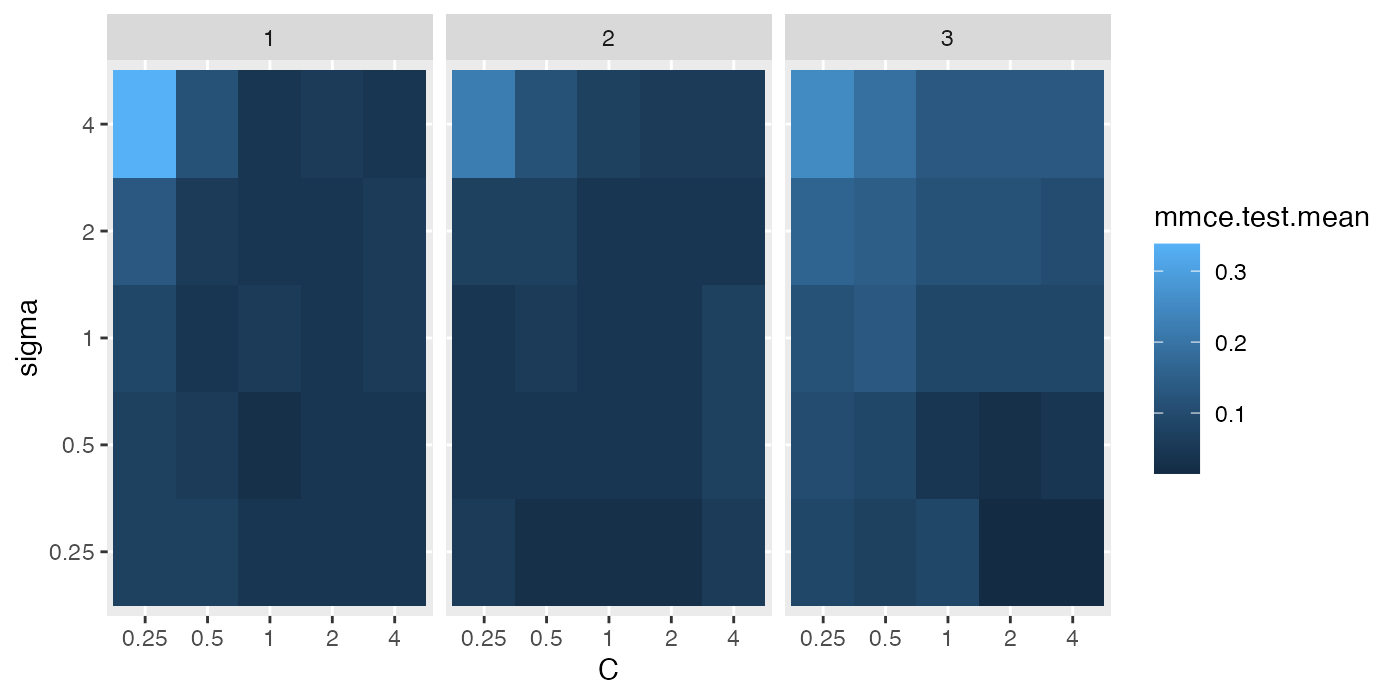
Another useful function is getNestedTuneResultsX(), which extracts the best found hyperparameter settings for each outer resampling iteration.
getNestedTuneResultsX(r)
## C sigma
## 1 1 0.50
## 2 2 0.25
## 3 2 0.25You can furthermore access the resampling indices of the inner level using getResamplingIndices() if you used either extract = getTuneResult or extract = getFeatSelResult in the resample() call:
getResamplingIndices(r, inner = TRUE)
## [[1]]
## [[1]]$train.inds
## [[1]]$train.inds[[1]]
## [1] 122 139 148 93 60 28 146 141 126 1 38 117 10 124 129 34 101 36 91
## [20] 2 99 33 42 61 51 87 96 54 7 132 115 113 32 150 41 40 64 69
## [39] 12 110 112 106 31 78 109 102 9 44 84 104 56 147 86 130 123 105 125
## [58] 70 133 135 142 58 128 111 16 55
##
## [[1]]$train.inds[[2]]
## [1] 36 136 118 93 123 2 117 75 33 109 98 62 116 144 56 150 28 1 82
## [20] 115 20 86 125 29 14 44 11 17 54 133 91 60 18 99 73 104 37 132
## [39] 9 7 61 68 87 65 106 50 130 147 16 38 114 139 12 145 70 124 134
## [58] 146 58 42 55 31 74 77 26 148
##
##
## [[1]]$test.inds
## [[1]]$test.inds[[1]]
## [1] 73 20 90 13 80 68 77 14 26 145 11 37 118 103 116 62 134 29 27
## [20] 98 65 30 18 100 82 144 22 50 74 17 5 75 114 136
##
## [[1]]$test.inds[[2]]
## [1] 141 69 90 41 34 112 13 80 103 84 32 110 142 27 122 30 135 113 102
## [20] 100 128 96 10 101 126 111 51 22 64 105 5 40 78 129
##
##
##
## [[2]]
## [[2]]$train.inds
## [[2]]$train.inds[[1]]
## [1] 143 56 119 108 48 49 85 43 120 24 135 146 149 114 12 133 40 36 6
## [20] 33 107 13 128 31 73 127 46 140 59 41 51 35 100 72 7 53 44 77
## [39] 150 20 105 74 90 118 52 92 79 137 3 57 16 121 87 45 76 80 30
## [58] 94 26 95 15 63 126 89 67 124
##
## [[2]]$train.inds[[2]]
## [1] 59 111 3 48 76 16 140 149 8 5 128 94 20 79 87 42 85 83 35
## [20] 138 62 56 21 44 121 25 135 18 144 114 45 89 127 36 88 81 101 92
## [39] 73 39 145 61 24 150 90 51 13 4 108 70 26 104 119 146 129 46 77
## [58] 17 133 97 23 107 120 63 143 118
##
##
## [[2]]$test.inds
## [[2]]$test.inds[[1]]
## [1] 5 17 19 18 55 61 25 47 4 131 129 101 144 88 81 99 62 70 145
## [20] 50 111 23 21 39 97 58 42 71 104 66 138 78 8 83
##
## [[2]]$test.inds[[2]]
## [1] 126 100 19 15 55 40 43 47 74 105 7 131 124 49 12 53 99 33 6
## [20] 50 41 52 58 67 31 71 66 57 78 95 72 80 137 30
##
##
##
## [[3]]
## [[3]]$train.inds
## [[3]]$train.inds[[1]]
## [1] 63 45 10 75 69 113 106 92 1 29 89 47 142 81 122 6 65 25 71
## [20] 53 60 120 93 136 9 143 110 48 79 86 19 3 57 24 67 123 66 131
## [39] 127 140 23 2 85 72 76 39 46 119 82 138 130 149 8 35 116 125 14
## [58] 34 117 15 64 4 98 27 148 103
##
## [[3]]$train.inds[[2]]
## [1] 125 140 119 147 84 79 96 47 69 93 3 91 131 95 43 35 134 110 45
## [20] 85 60 27 53 103 6 137 49 67 115 83 116 76 25 64 149 97 8 52
## [39] 34 89 28 1 66 21 19 29 11 32 112 9 120 4 108 102 10 127 117
## [58] 138 113 75 141 143 39 59 22 132
##
##
## [[3]]$test.inds
## [[3]]$test.inds[[1]]
## [1] 52 37 88 22 109 95 102 84 132 83 134 141 115 121 108 54 94 112 32
## [20] 38 43 139 147 49 28 59 21 97 68 107 91 137 96 11
##
## [[3]]$test.inds[[2]]
## [1] 130 122 14 37 63 92 82 88 109 57 24 71 72 121 81 142 54 46 94
## [20] 98 48 38 23 139 86 2 148 15 68 107 136 123 106 65Feature selection
As you might recall from the section about feature selection, mlr supports the filter and the wrapper approach.
Wrapper methods
Wrapper methods use the performance of a learning algorithm to assess the usefulness of a feature set. In order to select a feature subset a learner is trained repeatedly on different feature subsets and the subset which leads to the best learner performance is chosen.
For feature selection in the inner resampling loop, you need to choose a search strategy (function makeFeatSelControl* (FeatSelControl())), a performance measure and the inner resampling strategy. Then use function makeFeatSelWrapper() to bind everything together.
Below we use sequential forward selection with linear regression on the BostonHousing (mlbench::BostonHousing() data set (bh.task()).
# Feature selection in inner resampling loop
inner = makeResampleDesc("CV", iters = 3)
lrn = makeFeatSelWrapper("regr.lm",
resampling = inner,
control = makeFeatSelControlSequential(method = "sfs"), show.info = FALSE)
# Outer resampling loop
outer = makeResampleDesc("Subsample", iters = 2)
r = resample(
learner = lrn, task = bh.task, resampling = outer, extract = getFeatSelResult,
show.info = FALSE)
r
## Resample Result
## Task: BostonHousing-example
## Learner: regr.lm.featsel
## Aggr perf: mse.test.mean=24.8753005
## Runtime: 7.01506
r$measures.test
## iter mse
## 1 1 22.28967
## 2 2 27.46093Accessing the selected features
The result of the feature selection can be extracted by function getFeatSelResult(). It is also possible to keep whole models (makeWrappedModel()) by setting models = TRUE when calling resample().
r$extract
## [[1]]
## FeatSel result:
## Features (8): zn, chas, nox, rm, dis, ptratio, b, lstat
## mse.test.mean=26.8943900
##
## [[2]]
## FeatSel result:
## Features (10): crim, zn, nox, rm, dis, rad, tax, ptratio, b, l...
## mse.test.mean=21.5240684
# Selected features in the first outer resampling iteration
r$extract[[1]]$x
## [1] "zn" "chas" "nox" "rm" "dis" "ptratio" "b"
## [8] "lstat"
# Resampled performance of the selected feature subset on the first inner training set
r$extract[[1]]$y
## mse.test.mean
## 26.89439As for tuning, you can extract the optimization paths. The resulting data.frames contain, among others, binary columns for all features, indicating if they were included in the linear regression model, and the corresponding performances.
opt.paths = lapply(r$extract, function(x) as.data.frame(x$opt.path))
head(opt.paths[[1]])
## crim zn indus chas nox rm age dis rad tax ptratio b lstat mse.test.mean
## 1 0 0 0 0 0 0 0 0 0 0 0 0 0 84.52018
## 2 1 0 0 0 0 0 0 0 0 0 0 0 0 95.46348
## 3 0 1 0 0 0 0 0 0 0 0 0 0 0 74.97858
## 4 0 0 1 0 0 0 0 0 0 0 0 0 0 66.35546
## 5 0 0 0 1 0 0 0 0 0 0 0 0 0 81.49228
## 6 0 0 0 0 1 0 0 0 0 0 0 0 0 67.72664
## dob eol error.message exec.time
## 1 1 2 <NA> 0.031
## 2 2 2 <NA> 0.037
## 3 2 2 <NA> 0.027
## 4 2 2 <NA> 0.030
## 5 2 2 <NA> 0.032
## 6 2 2 <NA> 0.031An easy-to-read version of the optimization path for sequential feature selection can be obtained with function analyzeFeatSelResult().
analyzeFeatSelResult(r$extract[[1]])
## Features : 8
## Performance : mse.test.mean=26.8943900
## zn, chas, nox, rm, dis, ptratio, b, lstat
##
## Path to optimum:
## - Features: 0 Init : Perf = 91.377 Diff: NA *
## - Features: 1 Add : lstat Perf = 40.871 Diff: 50.506 *
## - Features: 2 Add : rm Perf = 34.606 Diff: 6.265 *
## - Features: 3 Add : ptratio Perf = 31.673 Diff: 2.9328 *
## - Features: 4 Add : dis Perf = 30.535 Diff: 1.1381 *
## - Features: 5 Add : nox Perf = 28.968 Diff: 1.5667 *
## - Features: 6 Add : zn Perf = 27.993 Diff: 0.97562 *
## - Features: 7 Add : b Perf = 27.253 Diff: 0.73917 *
## - Features: 8 Add : chas Perf = 26.894 Diff: 0.35905 *
##
## Stopped, because no improving feature was found.Filter methods with tuning
Filter methods assign an importance value to each feature. Based on these values you can select a feature subset by either keeping all features with importance higher than a certain threshold or by keeping a fixed number or percentage of the highest ranking features. Often, neither the theshold nor the number or percentage of features is known in advance and thus tuning is necessary.
In the example below the threshold value (fw.threshold) is tuned in the inner resampling loop. For this purpose the base Learner (makeLearner()) "regr.lm" is wrapped two times. First, makeFilterWrapper() is used to fuse linear regression with a feature filtering preprocessing step. Then a tuning step is added by makeTuneWrapper().
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
# Tuning of the percentage of selected filters in the inner loop
lrn = makeFilterWrapper(learner = "regr.lm", fw.method = "FSelectorRcpp_information.gain")
ps = makeParamSet(makeDiscreteParam("fw.threshold", values = seq(0, 1, 0.2)))
ctrl = makeTuneControlGrid()
inner = makeResampleDesc("CV", iters = 3)
lrn = makeTuneWrapper(lrn, resampling = inner, par.set = ps, control = ctrl, show.info = FALSE)
# Outer resampling loop
outer = makeResampleDesc("CV", iters = 3)
r = resample(learner = lrn, task = bh.task, resampling = outer, models = TRUE, show.info = FALSE)
r
## Resample Result
## Task: BostonHousing-example
## Learner: regr.lm.filtered.tuned
## Aggr perf: mse.test.mean=23.5449481
## Runtime: 3.85235Accessing the selected features and optimal percentage
In the above example we kept the complete model (makeWrappedModel())s.
Below are some examples that show how to extract information from the model (makeWrappedModel())s.
r$models
## [[1]]
## Model for learner.id=regr.lm.filtered.tuned; learner.class=TuneWrapper
## Trained on: task.id = BostonHousing-example; obs = 337; features = 13
## Hyperparameters: fw.method=FSelectorRcp...
##
## [[2]]
## Model for learner.id=regr.lm.filtered.tuned; learner.class=TuneWrapper
## Trained on: task.id = BostonHousing-example; obs = 337; features = 13
## Hyperparameters: fw.method=FSelectorRcp...
##
## [[3]]
## Model for learner.id=regr.lm.filtered.tuned; learner.class=TuneWrapper
## Trained on: task.id = BostonHousing-example; obs = 338; features = 13
## Hyperparameters: fw.method=FSelectorRcp...The result of the feature selection can be extracted by function getFilteredFeatures(). Almost always all 13 features are selected.
lapply(r$models, function(x) getFilteredFeatures(x$learner.model$next.model))
## [[1]]
## [1] "crim" "zn" "indus" "chas" "nox" "rm" "age"
## [8] "dis" "rad" "tax" "ptratio" "b" "lstat"
##
## [[2]]
## [1] "crim" "zn" "indus" "chas" "nox" "rm" "age"
## [8] "dis" "rad" "tax" "ptratio" "b" "lstat"
##
## [[3]]
## [1] "crim" "zn" "indus" "chas" "nox" "rm" "age"
## [8] "dis" "rad" "tax" "ptratio" "b" "lstat"Below the tune results (TuneResult()) and optimization paths (ParamHelpers::OptPath()) are accessed.
res = lapply(r$models, getTuneResult)
res
## [[1]]
## Tune result:
## Op. pars: fw.threshold=0
## mse.test.mean=24.0256189
##
## [[2]]
## Tune result:
## Op. pars: fw.threshold=0
## mse.test.mean=22.3639004
##
## [[3]]
## Tune result:
## Op. pars: fw.threshold=0
## mse.test.mean=25.7198156
opt.paths = lapply(res, function(x) as.data.frame(x$opt.path))
opt.paths[[1]][, -ncol(opt.paths[[1]])]
## fw.threshold mse.test.mean dob eol error.message
## 1 0 24.02562 1 NA <NA>
## 2 0.2 67.30442 2 NA <NA>
## 3 0.4 67.82551 3 NA <NA>
## 4 0.6 67.82551 4 NA <NA>
## 5 0.8 67.82551 5 NA <NA>
## 6 1 67.82551 6 NA <NA>Benchmark experiments
In a benchmark experiment multiple learners are compared on one or several tasks (see also the section about benchmarking. Nested resampling in benchmark experiments is achieved the same way as in resampling:
- First, use
makeTuneWrapper()ormakeFeatSelWrapper()to generate wrapped Learner (makeLearner())s with the inner resampling strategies of your choice. - Second, call
benchmark()and specify the outer resampling strategies for all tasks.
The inner resampling strategies should be resample descriptions (makeResampleDesc()). You can use different inner resampling strategies for different wrapped learners. For example it might be practical to do fewer subsampling or bootstrap iterations for slower learners.
If you have larger benchmark experiments you might want to have a look at the section about parallelization.
As mentioned in the section about benchmark experiments you can also use different resampling strategies for different learning tasks by passing a list of resampling descriptions or instances to benchmark().
We will see three examples to show different benchmark settings:
- Two data sets + two classification algorithms + tuning
- One data set + two regression algorithms + feature selection
- One data set + two regression algorithms + feature filtering + tuning
Example 1: Two tasks, two learners, tuning
Below is a benchmark experiment with two data sets, datasets::iris() and mlbench::sonar(), and two Learner (makeLearner())s, kernlab::ksvm() and kknn::kknn(), that are both tuned.
As inner resampling strategies we use holdout for kernlab::ksvm() and subsampling with 3 iterations for kknn::kknn(). As outer resampling strategies we take holdout for the datasets::iris() and bootstrap with 2 iterations for the mlbench::sonar() data (sonar.task()). We consider the accuracy (acc), which is used as tuning criterion, and also calculate the balanced error rate (ber).
# List of learning tasks
tasks = list(iris.task, sonar.task)
# Tune svm in the inner resampling loop
ps = makeParamSet(
makeDiscreteParam("C", 2^(-1:1)),
makeDiscreteParam("sigma", 2^(-1:1)))
ctrl = makeTuneControlGrid()
inner = makeResampleDesc("Holdout")
lrn1 = makeTuneWrapper("classif.ksvm",
resampling = inner, par.set = ps, control = ctrl,
show.info = FALSE)
# Tune k-nearest neighbor in inner resampling loop
ps = makeParamSet(makeDiscreteParam("k", 3:5))
ctrl = makeTuneControlGrid()
inner = makeResampleDesc("Subsample", iters = 3)
lrn2 = makeTuneWrapper("classif.kknn",
resampling = inner, par.set = ps, control = ctrl,
show.info = FALSE)
## Loading required package: kknn
# Learners
lrns = list(lrn1, lrn2)
# Outer resampling loop
outer = list(makeResampleDesc("Holdout"), makeResampleDesc("Bootstrap", iters = 2))
res = benchmark(lrns, tasks, outer,
measures = list(acc, ber), show.info = FALSE,
keep.extract = TRUE)
res
## task.id learner.id acc.test.mean ber.test.mean
## 1 iris-example classif.ksvm.tuned 0.9800000 0.02222222
## 2 iris-example classif.kknn.tuned 0.9600000 0.04305556
## 3 Sonar-example classif.ksvm.tuned 0.4903819 0.50000000
## 4 Sonar-example classif.kknn.tuned 0.8725237 0.12827855The print method for the BenchmarkResult() shows the aggregated performances from the outer resampling loop.
As you might recall, mlr offers several accessor function to extract information from the benchmark result. These are listed on the help page of BenchmarkResult() and many examples are shown on the tutorial page about benchmark experiments.
The performance values in individual outer resampling runs can be obtained by getBMRPerformances(). Note that, since we used different outer resampling strategies for the two tasks, the number of rows per task differ.
getBMRPerformances(res, as.df = TRUE)
## task.id learner.id iter acc ber
## 1 iris-example classif.ksvm.tuned 1 0.9800000 0.02222222
## 2 iris-example classif.kknn.tuned 1 0.9600000 0.04305556
## 3 Sonar-example classif.ksvm.tuned 1 0.5116279 0.50000000
## 4 Sonar-example classif.ksvm.tuned 2 0.4691358 0.50000000
## 5 Sonar-example classif.kknn.tuned 1 0.9302326 0.07142857
## 6 Sonar-example classif.kknn.tuned 2 0.8148148 0.18512852The results from the parameter tuning can be obtained through function getBMRTuneResults().
getBMRTuneResults(res)
## $`iris-example`
## $`iris-example`$classif.ksvm.tuned
## $`iris-example`$classif.ksvm.tuned[[1]]
## Tune result:
## Op. pars: C=2; sigma=0.5
## mmce.test.mean=0.0294118
##
##
## $`iris-example`$classif.kknn.tuned
## $`iris-example`$classif.kknn.tuned[[1]]
## Tune result:
## Op. pars: k=5
## mmce.test.mean=0.0392157
##
##
##
## $`Sonar-example`
## $`Sonar-example`$classif.ksvm.tuned
## $`Sonar-example`$classif.ksvm.tuned[[1]]
## Tune result:
## Op. pars: C=1; sigma=2
## mmce.test.mean=0.2285714
##
## $`Sonar-example`$classif.ksvm.tuned[[2]]
## Tune result:
## Op. pars: C=0.5; sigma=0.5
## mmce.test.mean=0.2714286
##
##
## $`Sonar-example`$classif.kknn.tuned
## $`Sonar-example`$classif.kknn.tuned[[1]]
## Tune result:
## Op. pars: k=5
## mmce.test.mean=0.0714286
##
## $`Sonar-example`$classif.kknn.tuned[[2]]
## Tune result:
## Op. pars: k=4
## mmce.test.mean=0.0666667As for several other accessor functions a clearer representation as data.frame can be achieved by setting as.df = TRUE.
getBMRTuneResults(res, as.df = TRUE)
## task.id learner.id iter C sigma mmce.test.mean k
## 1 iris-example classif.ksvm.tuned 1 2.0 0.5 0.02941176 NA
## 2 iris-example classif.kknn.tuned 1 NA NA 0.03921569 5
## 3 Sonar-example classif.ksvm.tuned 1 1.0 2.0 0.22857143 NA
## 4 Sonar-example classif.ksvm.tuned 2 0.5 0.5 0.27142857 NA
## 5 Sonar-example classif.kknn.tuned 1 NA NA 0.07142857 5
## 6 Sonar-example classif.kknn.tuned 2 NA NA 0.06666667 4It is also possible to extract the tuning results for individual tasks and learners and, as shown in earlier examples, inspect the optimization path (ParamHelpers::OptPath()).
tune.res = getBMRTuneResults(res,
task.ids = "Sonar-example", learner.ids = "classif.ksvm.tuned",
as.df = TRUE)
tune.res
## task.id learner.id iter C sigma mmce.test.mean
## 1 Sonar-example classif.ksvm.tuned 1 1.0 2.0 0.2285714
## 2 Sonar-example classif.ksvm.tuned 2 0.5 0.5 0.2714286
getNestedTuneResultsOptPathDf(res$results[["Sonar-example"]][["classif.ksvm.tuned"]])
## C sigma mmce.test.mean dob eol error.message exec.time iter
## 1 0.5 0.5 0.2285714 1 NA <NA> 0.031 1
## 2 1 0.5 0.2285714 2 NA <NA> 0.032 1
## 3 2 0.5 0.2285714 3 NA <NA> 0.032 1
## 4 0.5 1 0.2285714 4 NA <NA> 0.033 1
## 5 1 1 0.2285714 5 NA <NA> 0.033 1
## 6 2 1 0.2285714 6 NA <NA> 0.034 1
## 7 0.5 2 0.2285714 7 NA <NA> 0.045 1
## 8 1 2 0.2285714 8 NA <NA> 0.032 1
## 9 2 2 0.2285714 9 NA <NA> 0.031 1
## 10 0.5 0.5 0.2714286 1 NA <NA> 0.033 2
## 11 1 0.5 0.2714286 2 NA <NA> 0.033 2
## 12 2 0.5 0.2714286 3 NA <NA> 0.044 2
## 13 0.5 1 0.2714286 4 NA <NA> 0.032 2
## 14 1 1 0.2714286 5 NA <NA> 0.032 2
## 15 2 1 0.2714286 6 NA <NA> 0.032 2
## 16 0.5 2 0.2714286 7 NA <NA> 0.031 2
## 17 1 2 0.2714286 8 NA <NA> 0.032 2
## 18 2 2 0.2714286 9 NA <NA> 0.043 2Example 2: One task, two learners, feature selection
Let’s see how we can do feature selection in a benchmark experiment:
# Feature selection in inner resampling loop
ctrl = makeFeatSelControlSequential(method = "sfs")
inner = makeResampleDesc("Subsample", iters = 2)
lrn = makeFeatSelWrapper("regr.lm", resampling = inner, control = ctrl, show.info = FALSE)
# Learners
lrns = list("regr.rpart", lrn)
# Outer resampling loop
outer = makeResampleDesc("Subsample", iters = 2)
res = benchmark(
tasks = bh.task, learners = lrns, resampling = outer,
show.info = FALSE, keep.extract = TRUE)
res
## task.id learner.id mse.test.mean
## 1 BostonHousing-example regr.rpart 23.58119
## 2 BostonHousing-example regr.lm.featsel 24.75507The selected features can be extracted by function getBMRFeatSelResults(). By default, a nested list, with the first level indicating the task and the second level indicating the learner, is returned. If only a single learner or, as in our case, a single task is considered, setting drop = TRUE simplifies the result to a flat list.
getBMRFeatSelResults(res)
## $`BostonHousing-example`
## $`BostonHousing-example`$regr.rpart
## NULL
##
## $`BostonHousing-example`$regr.lm.featsel
## $`BostonHousing-example`$regr.lm.featsel[[1]]
## FeatSel result:
## Features (7): indus, rm, age, dis, ptratio, b, lstat
## mse.test.mean=29.4228023
##
## $`BostonHousing-example`$regr.lm.featsel[[2]]
## FeatSel result:
## Features (9): zn, indus, chas, nox, rm, dis, ptratio, b, lstat
## mse.test.mean=26.1964766
getBMRFeatSelResults(res, drop = TRUE)
## $regr.rpart
## NULL
##
## $regr.lm.featsel
## $regr.lm.featsel[[1]]
## FeatSel result:
## Features (7): indus, rm, age, dis, ptratio, b, lstat
## mse.test.mean=29.4228023
##
## $regr.lm.featsel[[2]]
## FeatSel result:
## Features (9): zn, indus, chas, nox, rm, dis, ptratio, b, lstat
## mse.test.mean=26.1964766You can access results for individual learners and tasks and inspect them further.
feats = getBMRFeatSelResults(res, learner.id = "regr.lm.featsel", drop = TRUE)
# Selected features in the first outer resampling iteration
feats[[1]]$x
## [1] "indus" "rm" "age" "dis" "ptratio" "b" "lstat"
# Resampled performance of the selected feature subset on the first inner training set
feats[[1]]$y
## mse.test.mean
## 29.4228As for tuning, you can extract the optimization paths. The resulting data.frames contain, among others, binary columns for all features, indicating if they were included in the linear regression model, and the corresponding performances. analyzeFeatSelResult() gives a clearer overview.
opt.paths = lapply(feats, function(x) as.data.frame(x$opt.path))
head(opt.paths[[1]][, -ncol(opt.paths[[1]])])
## crim zn indus chas nox rm age dis rad tax ptratio b lstat mse.test.mean dob
## 1 0 0 0 0 0 0 0 0 0 0 0 0 0 80.74823 1
## 2 1 0 0 0 0 0 0 0 0 0 0 0 0 70.11222 2
## 3 0 1 0 0 0 0 0 0 0 0 0 0 0 71.63520 2
## 4 0 0 1 0 0 0 0 0 0 0 0 0 0 64.69041 2
## 5 0 0 0 1 0 0 0 0 0 0 0 0 0 83.04175 2
## 6 0 0 0 0 1 0 0 0 0 0 0 0 0 68.37808 2
## eol error.message
## 1 2 <NA>
## 2 2 <NA>
## 3 2 <NA>
## 4 2 <NA>
## 5 2 <NA>
## 6 2 <NA>
analyzeFeatSelResult(feats[[1]])
## Features : 7
## Performance : mse.test.mean=29.4228023
## indus, rm, age, dis, ptratio, b, lstat
##
## Path to optimum:
## - Features: 0 Init : Perf = 80.748 Diff: NA *
## - Features: 1 Add : lstat Perf = 37.629 Diff: 43.119 *
## - Features: 2 Add : rm Perf = 32.289 Diff: 5.3397 *
## - Features: 3 Add : dis Perf = 31.4 Diff: 0.88931 *
## - Features: 4 Add : indus Perf = 30.321 Diff: 1.0794 *
## - Features: 5 Add : ptratio Perf = 29.775 Diff: 0.54598 *
## - Features: 6 Add : b Perf = 29.469 Diff: 0.3058 *
## - Features: 7 Add : age Perf = 29.423 Diff: 0.046036 *
##
## Stopped, because no improving feature was found.Example 3: One task, two learners, feature filtering with tuning
Here is a minimal example for feature filtering with tuning of the feature subset size.
# Feature filtering with tuning in the inner resampling loop
lrn = makeFilterWrapper(learner = "regr.lm", fw.method = "FSelectorRcpp_information.gain")
ps = makeParamSet(makeDiscreteParam("fw.abs", values = seq_len(getTaskNFeats(bh.task))))
ctrl = makeTuneControlGrid()
inner = makeResampleDesc("CV", iter = 2)
lrn = makeTuneWrapper(lrn,
resampling = inner, par.set = ps, control = ctrl,
show.info = FALSE)
# Learners
lrns = list("regr.rpart", lrn)
# Outer resampling loop
outer = makeResampleDesc("Subsample", iter = 3)
res = benchmark(tasks = bh.task, learners = lrns, resampling = outer, show.info = FALSE)
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
## Warning in .information_gain.data.frame(x = x, y = y, type = type, equal =
## equal, : Dependent variable is a numeric! It will be converted to factor with
## simple factor(y). We do not discretize dependent variable in FSelectorRcpp by
## default! You can choose equal frequency binning discretization by setting equal
## argument to TRUE.
res
## task.id learner.id mse.test.mean
## 1 BostonHousing-example regr.rpart 22.16021
## 2 BostonHousing-example regr.lm.filtered.tuned 27.79428
# Performances on individual outer test data sets
getBMRPerformances(res, as.df = TRUE)
## task.id learner.id iter mse
## 1 BostonHousing-example regr.rpart 1 23.14016
## 2 BostonHousing-example regr.rpart 2 29.91067
## 3 BostonHousing-example regr.rpart 3 13.42981
## 4 BostonHousing-example regr.lm.filtered.tuned 1 29.75924
## 5 BostonHousing-example regr.lm.filtered.tuned 2 38.05312
## 6 BostonHousing-example regr.lm.filtered.tuned 3 15.57047