Training a Learner

Training a learner means fitting a model to a given data set. In mlr this can be done by calling function train() on a Learner (makeLearner()) and a suitable Task().

We start with a classification example and perform a linear discriminant analysis (MASS::lda()) on the iris (datasets::iris()) data set.

# Generate the task
task = makeClassifTask(data = iris, target = "Species")

# Generate the learner
lrn = makeLearner("classif.lda")

# Train the learner
mod = train(lrn, task)
mod
## Model for learner.id=classif.lda; learner.class=classif.lda
## Trained on: task.id = iris; obs = 150; features = 4
## Hyperparameters:

In the above example creating the Learner (makeLearner()) explicitly is not absolutely necessary. As a general rule, you have to generate the Learner (makeLearner()) yourself if you want to change any defaults, e.g., setting hyperparameter values or altering the predict type. Otherwise, train() and many other functions also accept the class name of the learner and call makeLearner() internally with default settings.

mod = train("classif.lda", task)
mod
## Model for learner.id=classif.lda; learner.class=classif.lda
## Trained on: task.id = iris; obs = 150; features = 4
## Hyperparameters:

Training a learner works the same way for every type of learning problem. Below is a survival analysis example where a Cox proportional hazards model (survival::coxph()) is fitted to the survival::lung() data set. Note that we use the corresponding lung.task() provided by mlr. All available Task()s are listed in the Appendix.

mod = train("surv.coxph", lung.task)
mod
## Model for learner.id=surv.coxph; learner.class=surv.coxph
## Trained on: task.id = lung-example; obs = 167; features = 8
## Hyperparameters:

Accessing learner models

Function train() returns an object of class WrappedModel (makeWrappedModel()), which encapsulates the fitted model, i.e., the output of the underlying R learning method. Additionally, it contains some information about the Learner (makeLearner()), the Task(), the features and observations used for training, and the training time. A WrappedModel (makeWrappedModel()) can subsequently be used to make a prediction (predict.WrappedModel()) for new observations.

The fitted model in slot $learner.model of the WrappedModel (makeWrappedModel()) object can be accessed using function getLearnerModel.

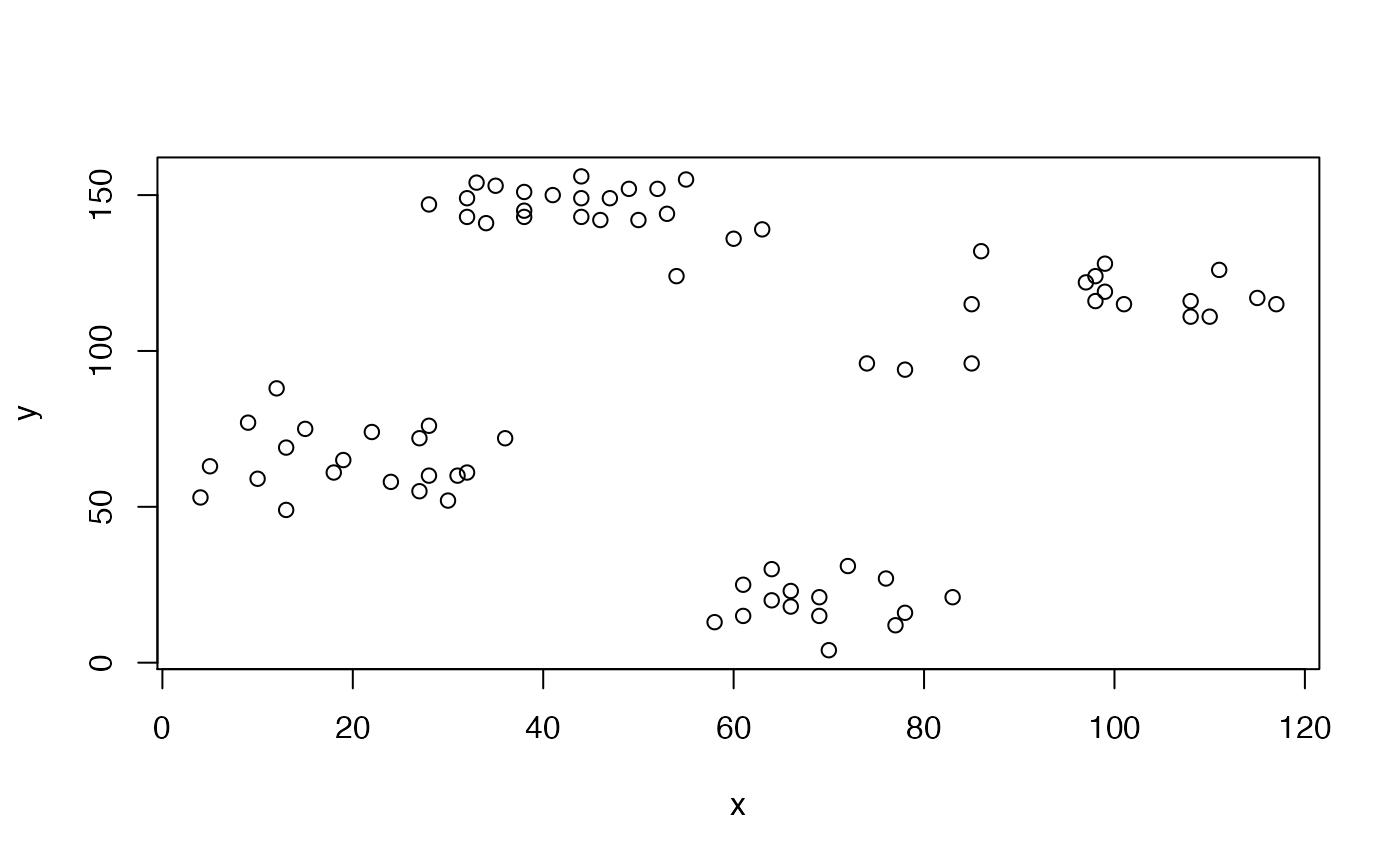
In the following example we cluster the Ruspini (cluster::ruspini()) data set (which has four groups and two features) by \(K\)-means with \(K = 4\) and extract the output of the underlying stats::kmeans() function.

data(ruspini, package = "cluster")
plot(y ~ x, ruspini)

# Generate the task
ruspini.task = makeClusterTask(data = ruspini)

# Generate the learner
lrn = makeLearner("cluster.kmeans", centers = 4)

# Train the learner
mod = train(lrn, ruspini.task)
mod
## Model for learner.id=cluster.kmeans; learner.class=cluster.kmeans
## Trained on: task.id = ruspini; obs = 75; features = 2
## Hyperparameters: centers=4

# Peak into mod
names(mod)
## [1] "learner"       "learner.model" "task.desc"     "subset"       
## [5] "features"      "factor.levels" "time"          "dump"

mod$learner
## Learner cluster.kmeans from package stats,clue
## Type: cluster
## Name: K-Means; Short name: kmeans
## Class: cluster.kmeans
## Properties: numerics,prob
## Predict-Type: response
## Hyperparameters: centers=4

mod$features
## [1] "x" "y"

# Extract the fitted model
getLearnerModel(mod)
## K-means clustering with 4 clusters of sizes 23, 17, 20, 15
## 
## Cluster means:
##          x        y
## 1 43.91304 146.0435
## 2 98.17647 114.8824
## 3 20.15000  64.9500
## 4 68.93333  19.4000
## 
## Clustering vector:
##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 
##  3  3  3  3  3  3  3  3  3  3  3  3  3  3  3  3  3  3  3  3  1  1  1  1  1  1 
## 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 
##  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  2  2  2  2  2  2  2  2  2 
## 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 
##  2  2  2  2  2  2  2  2  4  4  4  4  4  4  4  4  4  4  4  4  4  4  4 
## 
## Within cluster sum of squares by cluster:
## [1] 3176.783 4558.235 3689.500 1456.533
##  (between_SS / total_SS =  94.7 %)
## 
## Available components:
## 
## [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
## [6] "betweenss"    "size"         "iter"         "ifault"

Further options and comments

By default, the whole data set in the Task() is used for training. The subset argument of train() takes a logical or integer vector that indicates which observations to use, for example if you want to split your data into a training and a test set or if you want to fit separate models to different subgroups in the data.

Below we fit a linear regression model (stats::lm()) to the BostonHousing (mlbench::BostonHousing()) data set (bh.task()) and randomly select 1/3 of the data set for training.

# Get the number of observations
n = getTaskSize(bh.task)

# Use 1/3 of the observations for training
train.set = sample(n, size = n/3)

# Train the learner
mod = train("regr.lm", bh.task, subset = train.set)
mod
## Model for learner.id=regr.lm; learner.class=regr.lm
## Trained on: task.id = BostonHousing-example; obs = 168; features = 13
## Hyperparameters:

Note, for later, that all standard resampling strategies are supported. Therefore you usually do not have to subset the data yourself.

Moreover, if the learner supports this, you can specify observation weights that reflect the relevance of observations in the training process. Weights can be useful in many regards, for example to express the reliability of the training observations, reduce the influence of outliers or, if the data were collected over a longer time period, increase the influence of recent data. In supervised classification weights can be used to incorporate misclassification costs or account for class imbalance.

For example in the mlbench::BreastCancer() data set class benign is almost twice as frequent as class malignant. In order to grant both classes equal importance in training the classifier we can weight the examples according to the inverse class frequencies in the data set as shown in the following R code.

# Calculate the observation weights
target = getTaskTargets(bc.task)
tab = as.numeric(table(target))
w = 1/tab[target]

train("classif.rpart", task = bc.task, weights = w)
## Model for learner.id=classif.rpart; learner.class=classif.rpart
## Trained on: task.id = BreastCancer-example; obs = 683; features = 9
## Hyperparameters: xval=0

Note, for later, that mlr offers much more functionality to deal with imbalanced classification problems.

As another side remark for more advanced readers: By varying the weights in the calls to train(), you could also implement your own variant of a general boosting type algorithm on arbitrary mlr base learners.

As you may recall, it is also possible to set observation weights when creating the Task(). As a general rule, you should specify them in make*Task (Task()) if the weights really “belong” to the task and always should be used. Otherwise, pass them to train(). The weights in train() take precedence over the weights in Task().