Generate partial dependence.

Estimate how the learned prediction function is affected by one or more features. For a learned function f(x) where x is partitioned into x_s and x_c, the partial dependence of f on x_s can be summarized by averaging over x_c and setting x_s to a range of values of interest, estimating E_(x_c)(f(x_s, x_c)). The conditional expectation of f at observation i is estimated similarly. Additionally, partial derivatives of the marginalized function w.r.t. the features can be computed.

Usage

generatePartialDependenceData(
  obj,
  input,
  features = NULL,
  interaction = FALSE,
  derivative = FALSE,
  individual = FALSE,
  fun = mean,
  bounds = c(qnorm(0.025), qnorm(0.975)),
  uniform = TRUE,
  n = c(10, NA),
  ...
)

Arguments

obj

(WrappedModel)
Result of train.

input

(data.frame | Task)
Input data.

features

character
A vector of feature names contained in the training data. If not specified all features in the input will be used.

interaction

(logical(1))
Whether the features should be interacted or not. If TRUE then the Cartesian product of the prediction grid for each feature is taken, and the partial dependence at each unique combination of values of the features is estimated. Note that if the length of features is greater than two, plotPartialDependence cannot be used. If FALSE each feature is considered separately. In this case features can be much longer than two. Default is FALSE.

derivative

(logical(1))
Whether or not the partial derivative of the learned function with respect to the features should be estimated. If TRUE interaction must be FALSE. The partial derivative of individual observations may be estimated. Note that computation time increases as the learned prediction function is evaluated at gridsize points * the number of points required to estimate the partial derivative. Additional arguments may be passed to numDeriv::grad (for regression or survival tasks) or numDeriv::jacobian (for classification tasks). Note that functions which are not smooth may result in estimated derivatives of 0 (for points where the function does not change within +/- epsilon) or estimates trending towards +/- infinity (at discontinuities). Default is FALSE.

individual

(logical(1))
Whether to plot the individual conditional expectation curves rather than the aggregated curve, i.e., rather than aggregating (using fun) the partial dependences of features, plot the partial dependences of all observations in data across all values of the features. The algorithm is developed in Goldstein, Kapelner, Bleich, and Pitkin (2015). Default is FALSE.

fun

function

A function which operates on the output on the predictions made on the input data. For regression this means a numeric vector, and, e.g., for a multiclass classification problem, this migh instead be probabilities which are returned as a numeric matrix. This argument can return vectors of arbitrary length, however, if their length is greater than one, they must by named, e.g., fun = mean or fun = function(x) c("mean" = mean(x), "variance" = var(x)). The default is the mean, unless obj is classification with predict.type = "response" in which case the default is the proportion of observations predicted to be in each class.

bounds

(numeric(2))
The value (lower, upper) the estimated standard error is multiplied by to estimate the bound on a confidence region for a partial dependence. Ignored if predict.type != "se" for the learner. Default is the 2.5 and 97.5 quantiles (-1.96, 1.96) of the Gaussian distribution.

uniform

(logical(1))
Whether or not the prediction grid for the features is a uniform grid of size n[1] or sampled with replacement from the input. Default is TRUE.

n

(integer21)
The first element of n gives the size of the prediction grid created for each feature. The second element of n gives the size of the sample to be drawn without replacement from the input data. Setting n[2] less than the number of rows in the input will decrease computation time. The default for n[1] is 10, and the default for n[2] is the number of rows in the input.

...

additional arguments to be passed to mmpf::marginalPrediction.

Value

PartialDependenceData. A named list, which contains the partial dependence, input data, target, features, task description, and other arguments controlling the type of partial dependences made.

Object members:

data: data.frame
Has columns for the prediction: one column for regression and survival analysis, and a column for class and the predicted probability for classification as well as a a column for each element of features. If individual = TRUE then there is an additional column idx which gives the index of the data that each prediction corresponds to.
task.desc: TaskDesc
Task description.
target: Target feature for regression, target feature levels for classification, survival and event indicator for survival.
features: character
Features argument input.
interaction: (logical(1))
Whether or not the features were interacted (i.e. conditioning).
derivative: (logical(1))
Whether or not the partial derivative was estimated.
individual: (logical(1))
Whether the partial dependences were aggregated or the individual curves are retained.

References

Goldstein, Alex, Adam Kapelner, Justin Bleich, and Emil Pitkin. “Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation.” Journal of Computational and Graphical Statistics. Vol. 24, No. 1 (2015): 44-65.

Friedman, Jerome. “Greedy Function Approximation: A Gradient Boosting Machine.” The Annals of Statistics. Vol. 29. No. 5 (2001): 1189-1232.

Examples

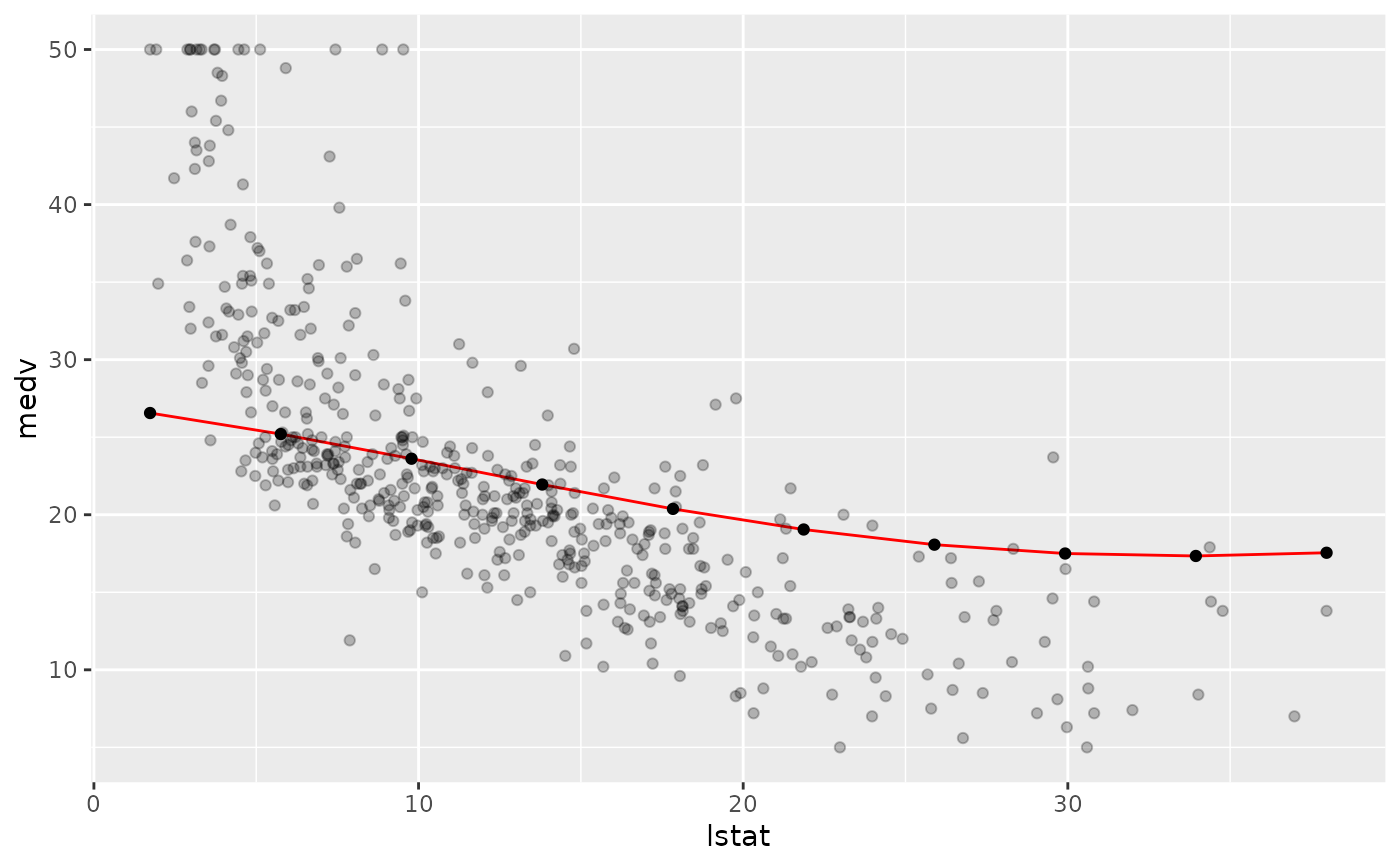
lrn = makeLearner("regr.svm")
fit = train(lrn, bh.task)
pd = generatePartialDependenceData(fit, bh.task, "lstat")
#> Loading required package: mmpf
plotPartialDependence(pd, data = getTaskData(bh.task))


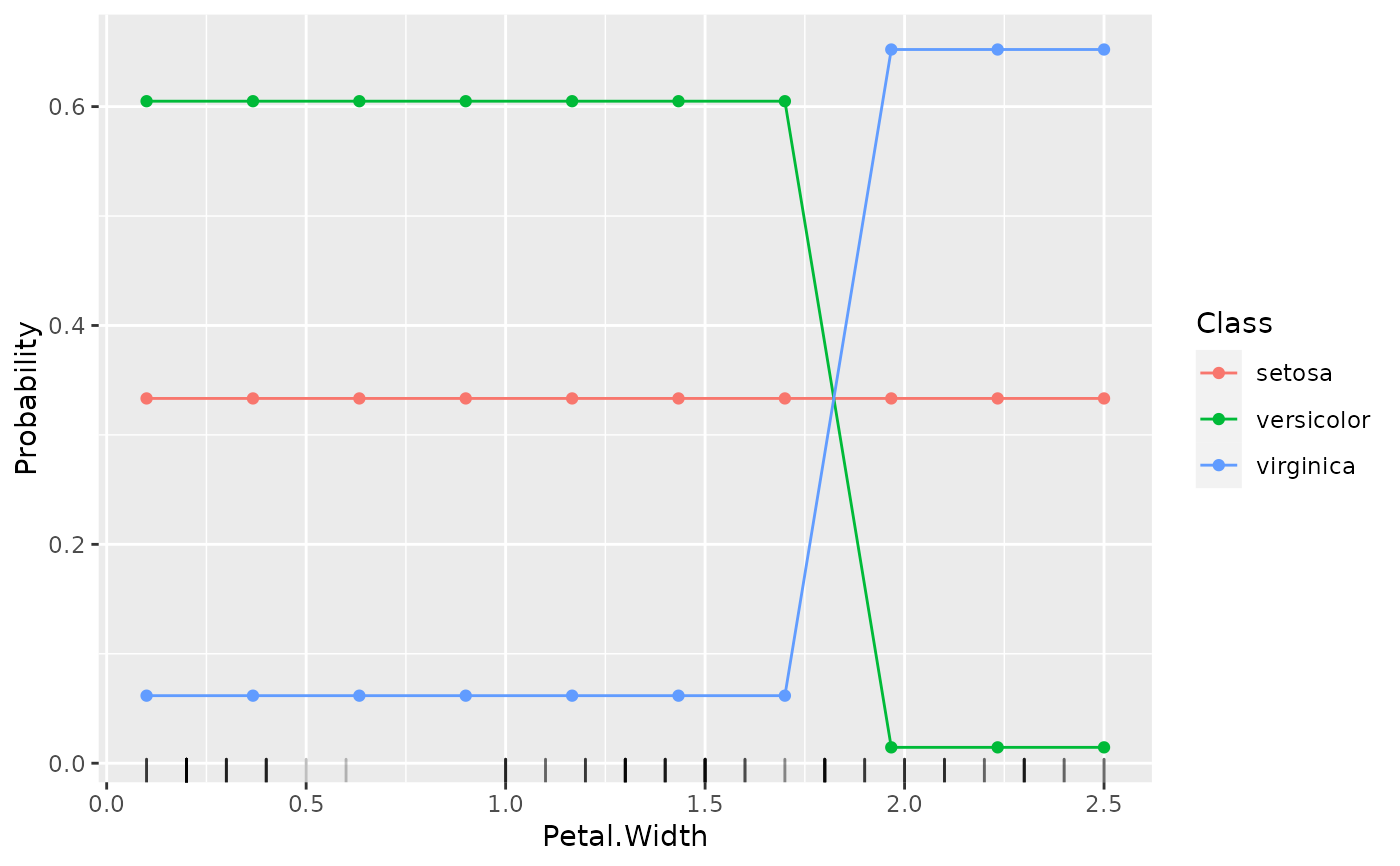
lrn = makeLearner("classif.rpart", predict.type = "prob")
fit = train(lrn, iris.task)
pd = generatePartialDependenceData(fit, iris.task, "Petal.Width")
plotPartialDependence(pd, data = getTaskData(iris.task))

Usage

Arguments

Value

References

See also

Examples